Bilangan Bulat

Pengertian Bilangan Bulat

Bilangan Bulat adalah himpunan bilangan yang terdiri dari bilangan bulat negatif, nol dan bilangan bulat positif.

Sehingga dapat disimpulkan bahwa bilangan bulat adalah himpunan bilangan yang mencakup bilangan cacah, bilangan asli, bilangan nol, bilangan satu, bilangan prima, bilangan komposit dan bilangan negatif.

Pengertian Bilangan Bulat Positif

Bilangan bulat positif adalah himpunan bilangan yang dimulai dari bilangan satu ke atas. Contoh bilangan bulat positif adalah: { 1, 2, 3, 4, 5, ….}

Pengertian bilangan bulat negatif
Bilangan bulat negatif adalah himpunan bilangan yang dimulai dari bilangan negatif satu ke bawah. Contoh bilangan bulat negatif adalah: { …. -5, -4, -3, -2, -1 }

Sehingga dapat ditarik kesimpulan bahwa cakupan dari himpunan bilangan bulat adalah himpunan bilangan bulat negatif, bilangan nol dan himpunan bilangan bulat positf.

Untuk lebih memahami tentang pengertian bilangan bulat, perhatikan gambar bagan di bawah ini!


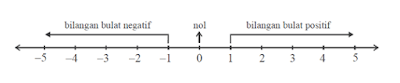
Hubungan Antara 2 Bilangan Bulat

Jika kalian amati pada garis bilangan di atas, jika ada 2 buah bilangan A dan B di tuliskan pada garis bilangan seperti di atas akan berlaku hubungan:
jika A terletak di sebelah kiri B maka nilai A lebih kecil dari nilai B ( A < B )
Jika A terletak di sebelah kanan B maka nilai A lebih besar dar nilaii B ( A > B )

Operasi Matematika

1. Penjumlahan
2 bilangan bulat bertanda sama:

Jika ada 2 buah bilangan bulat bertanda sama ( sama – sama negatif atau positif ). Jumlah kan kedua bilangan itu dan abaikan tanda ( + / – ).
2 bilangan bulat berlawanan tanda

Jika 2 buah bilangan berbeda tanda positif dan negatif, kurangi bilangan yang nilai nya besar dengan bilangan yang nilai nya kecil dengan abaikan tanda.

Sifat-sifat pada Penjumlahan Bilangan Bulat:
Sifat nya tertutup
Sifat nya komutatif atau pertukaran
Unsur nya identitias
Sifat nya asosiatif
Memiliki invers

2. Pengurangan

Pengurangan sama seperti penjumlahan lawan dari bilangan pengurang nya. perhatikan contoh berikut:

4 – 3 = 4 + ( -3 ) = 1

Kesimpulan nya pada pengurangan bilangan, mengurangi sebuah bilangan sama dengan menambah kan lawan bilangan pengurang itu sendiri.

Rumus nya:
a – b = a + ( -b )

3. Perkalian

rumus:
p x q = pg
( -p ) x q = –( p x q ) = -pq
p x ( -q ) = –( pxq ) = -pq
( -p ) x ( -q ) = p x q = pq

Sifat – sifat perkalian bilangan bulat:
Sifat nya tertutup
Sifat nya komutatif
Sifat nya asosiatif
Sifat nya distributif perkalian terhadap penjumlahan
Sifat nya distributif perkalian terhadap pengurangan
Unsur nya identitas

4. Pembagian

Operasi pembagian iyalah kebalikan dari operasi perkalian nya.
Jika = p : q = r

Maka:
p = q x r.

Tanda dalam pembagian bilangan bulat.
Jika dalam pembagian p : q = r maka:
jika p dan q bertanda sama maka r iyalah bilangan bulat positif
jika p dan q bertanda beda maka r iyalah bilangan bulat negatif.

Bagaimana jika di bagi 0? Berbeda dengan perkalian, jika a x 0 = 0 dalam pembagian a : 0 hasil nya tidak terdefinisi.

Sifat Pembagian Bilangan Bulat:
Tidak bersifat tertutup
Tidak bersifat komutatif
Tidak bersifat asosiatif